



Next: Coherent vortices
Up: Two-dimensional turbulence
Previous: Inverse energy cascade
Contents
On scales smaller than the forcing correlation length, the hypothesis
of a constant enstrophy flux
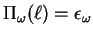 leads to a different scaling.
The enstrophy contained in the eddies of size
leads to a different scaling.
The enstrophy contained in the eddies of size 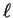 can
be estimated as
can
be estimated as
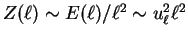 ,
and its flux
,
and its flux
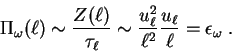 |
(1.72) |
gives the following scaling for velocities:
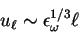 |
(1.73) |
Therefore the velocity field in the enstrophy cascade is smooth,
at variance with the velocity field in the inverse cascade.
The dimensional prediction for characteristic times simply tells
that there is essentially one single time scale in the
direct energy cascade
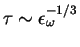 ,
which provides an estimate of the inverse of the Lyapunov
exponent of the flow.
The prediction for the energy spectrum reads
,
which provides an estimate of the inverse of the Lyapunov
exponent of the flow.
The prediction for the energy spectrum reads
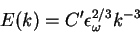 |
(1.74) |
Figure 1.5:
Energy spectrum of the direct enstrophy
cascade
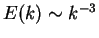 . In the scaling range
the enstrophy flux (shown in the inset) is almost constant.
. In the scaling range
the enstrophy flux (shown in the inset) is almost constant.
|
|
A spectrum 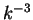 means that the integral
means that the integral
 , which measure the mean-square shear
has a logarithmic divergence in the infrared cutoff. Thus the
hypothesis of locality of interactions in the cascade can be violated
in the direct enstrophy cascade.
, which measure the mean-square shear
has a logarithmic divergence in the infrared cutoff. Thus the
hypothesis of locality of interactions in the cascade can be violated
in the direct enstrophy cascade.
In next chapter I will discuss how the presence of a linear drag
modifies this picture. We will show the presence of
small-scale intermittency for the statistics of vorticity
fluctuations and its dependence on the friction intensity.




Next: Coherent vortices
Up: Two-dimensional turbulence
Previous: Inverse energy cascade
Contents
Stefano Musacchio
2004-01-09
![]() leads to a different scaling.
The enstrophy contained in the eddies of size
leads to a different scaling.
The enstrophy contained in the eddies of size ![]() can
be estimated as
can
be estimated as
![]() ,
and its flux
,
and its flux
![\includegraphics[draft=false,scale=0.7]{P_campo_diretta512.eps}](img266.png)
![]() means that the integral
means that the integral
![]() , which measure the mean-square shear
has a logarithmic divergence in the infrared cutoff. Thus the
hypothesis of locality of interactions in the cascade can be violated
in the direct enstrophy cascade.
, which measure the mean-square shear
has a logarithmic divergence in the infrared cutoff. Thus the
hypothesis of locality of interactions in the cascade can be violated
in the direct enstrophy cascade.