



Next: Energy balance
Up: Navier-Stokes equation
Previous: Navier-Stokes equation
Contents
Reynolds number
A measure of the non-linearity of Navier-Stokes equations is given by the
Reynolds number
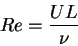 |
(1.7) |
where 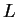 and
and 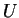 are respectively the typical length scale
and velocity of the fluid, e.g. in a pipe flow
are respectively the typical length scale
and velocity of the fluid, e.g. in a pipe flow 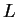 is the diameter
of the pipe and
is the diameter
of the pipe and 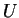 the mean velocity.
It was introduced by Osborne Reynolds, who showed that a transition
between laminar and turbulent flow occurs when the
the mean velocity.
It was introduced by Osborne Reynolds, who showed that a transition
between laminar and turbulent flow occurs when the 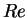 number reaches
a critical value. Different geometries of the flow may change
the critical
number reaches
a critical value. Different geometries of the flow may change
the critical 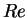 number, but the transition is
universally controlled by this adimensional parameter.
The Reynolds number plays a fundamental role in turbulence, since it
gives a dimensional estimate of the relative weight between the
inertial term
number, but the transition is
universally controlled by this adimensional parameter.
The Reynolds number plays a fundamental role in turbulence, since it
gives a dimensional estimate of the relative weight between the
inertial term
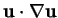 and the viscous term
and the viscous term
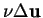 :
:
![\begin{displaymath}
{[{\mbox{\boldmath$u$}} \cdot \nabla {\mbox{\boldmath$u$}}] \over [\nu \Delta {\mbox{\boldmath$u$}}]}
\sim \frac{UL}{\nu}
\end{displaymath}](img91.png) |
(1.8) |
Because of its definition, the limit 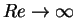 in which
fully developed turbulence is achieved, can be rephrased as
the zero-viscosity limit
in which
fully developed turbulence is achieved, can be rephrased as
the zero-viscosity limit 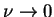 .
.




Next: Energy balance
Up: Navier-Stokes equation
Previous: Navier-Stokes equation
Contents
Stefano Musacchio
2004-01-09