Alcuni esempi che mostrano come usare gli algoritmi forniti da scipy.
Integrazione numerica¶
<\p>
<\p>
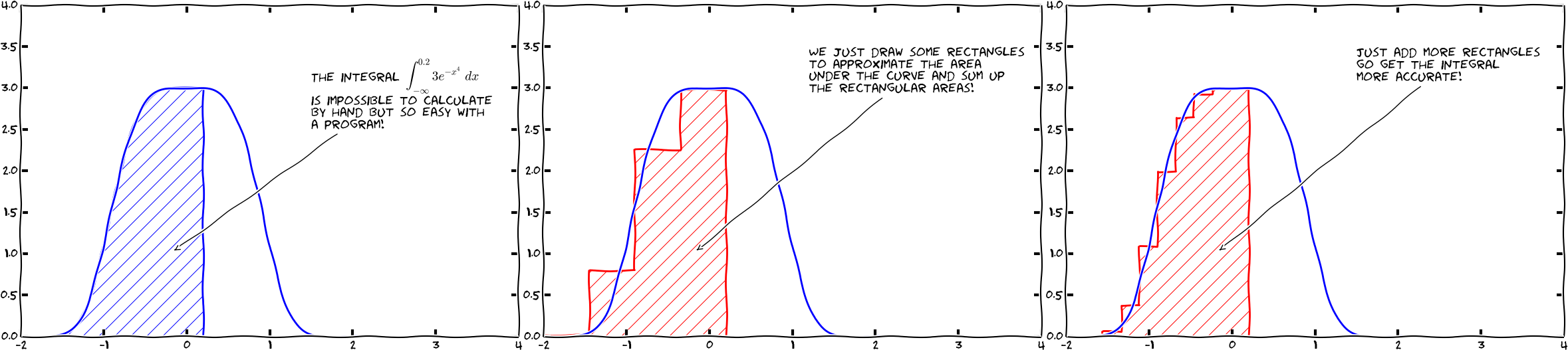 (Svein Linge, Hans Petter Langtangen - Programming for Computations)
(Svein Linge, Hans Petter Langtangen - Programming for Computations)
<\p>
<\p>
La libreria scipy (SCIentific PYthon) fornisce un gran numero di algoritmi numerici. In questo notebook vengono presentati quelli di uso più comune che servono a calcolare integrali, trovare zeri, massimi e minimi di funzioni, risolvere equazioni differenziali e interpolare dati.
Scipy è basata su numpy. Nella documentazione di scipy viene raccomandato di importare le due librerie separatamente.
import numpy as np
import scipy
La libreria scipy fornisce informazioni sulla propria struttura atrraverso il comando help:
help(scipy)
L'output è molto lungo. Ne mostriamo solo una parte:
stats --- Statistical Functions [*]
sparse --- Sparse matrix [*]
lib --- Python wrappers to external libraries [*]
linalg --- Linear algebra routines [*]
signal --- Signal Processing Tools [*]
misc --- Various utilities that don't have another home.
interpolate --- Interpolation Tools [*]
optimize --- Optimization Tools [*]
cluster --- Vector Quantization / Kmeans [*]
fftpack --- Discrete Fourier Transform algorithms [*]
io --- Data input and output [*]
integrate --- Integration routines [*]
lib.lapack --- Wrappers to LAPACK library [*]
special --- Special Functions [*]
lib.blas --- Wrappers to BLAS library [*]
[*] - using a package requires explicit import (see pkgload)Per trovare un algoritmo per integrare una funzione, si può esplorare la libreria integrate:
import scipy.integrate
scipy.integrate?
produces:
=============================================
Integration and ODEs (:mod:`scipy.integrate`)
=============================================
.. currentmodule:: scipy.integrate
Integrating functions, given function object
============================================
.. autosummary::
:toctree: generated/
quad -- General purpose integration
dblquad -- General purpose double integration
tplquad -- General purpose triple integration
nquad -- General purpose n-dimensional integration
fixed_quad -- Integrate func(x) using Gaussian quadrature of order n
quadrature -- Integrate with given tolerance using Gaussian quadrature
romberg -- Integrate func using Romberg integration
quad_explain -- Print information for use of quad
newton_cotes -- Weights and error coefficient for Newton-Cotes integration
IntegrationWarning -- Warning on issues during integration
Integrating functions, given fixed samples
==========================================
.. autosummary::
:toctree: generated/
trapz -- Use trapezoidal rule to compute integral.
cumtrapz -- Use trapezoidal rule to cumulatively compute integral.
simps -- Use Simpson's rule to compute integral from samples.
romb -- Use Romberg Integration to compute integral from
-- (2**k + 1) evenly-spaced samples.
.. seealso::
:mod:`scipy.special` for orthogonal polynomials (special) for Gaussian
quadrature roots and weights for other weighting factors and regions.
Integrators of ODE systems
==========================
.. autosummary::
:toctree: generated/
odeint -- General integration of ordinary differential equations.
ode -- Integrate ODE using VODE and ZVODE routines.
complex_ode -- Convert a complex-valued ODE to real-valued and integrate.
Alcuni esempi che mostrano come usare gli algoritmi forniti da scipy.
<\p>
<\p>
 (Svein Linge, Hans Petter Langtangen - Programming for Computations)
(Svein Linge, Hans Petter Langtangen - Programming for Computations)
<\p>
<\p>
Scientific Python fornisce diverse routines di integrazione. Uno strumento di uso generale per calcolare integrali I del tipo
$$I=\int_a^b f(x) \mathrm{d} x$$è la funzione quad() del modulo scipy.integrate.
Prende in input la funzione f(x) da integrare (l'“integrando”) e gli estremi inferiore e superiore a and b. Restituisce due valori, (in una tuple): il primo è il risultato dell'integrale mentre il secondo è una stima dell'errore numerico del risultato.
from scipy import integrate
help(integrate.quad)
Ecco un esempio: $$I=\int_{-2}^{2} e^{\cos(-2 \pi x)} \,\mathrm{d} x$$
from math import cos, exp, pi
from scipy.integrate import quad
# funzione da integrare
def f(x):
return exp(cos(-2 * x * pi))
# chiamata a quad
res, err = quad(f, -2, 2)
print(f"The numerical result is {res:f} (+-{err:g})")
Usando Numpy:
import numpy as np
def f_N(x):
return np.exp(np.cos(-2 * x * np.pi))
res, err = quad(f_N, -2, 2)
print(f"The numerical result is {res:f} (+-{err:g})")
Si noti che quad() può prendere come parametri opzionali epsabs e epsrel per aumentare o diminuire l'accuratezza del calcolo (Usate help(quad) per maggiori informazioni). I valori di default sono epsabs=1.5e-8 and epsrel=1.5e-8. Per il prossimo esercizio, i valori di default sono sufficienti.
def my_f(x):
return 1/x/x
res, err = quad(my_f, 1, np.inf)
print(f"The numerical result is {res:f} (+-{err:g})")
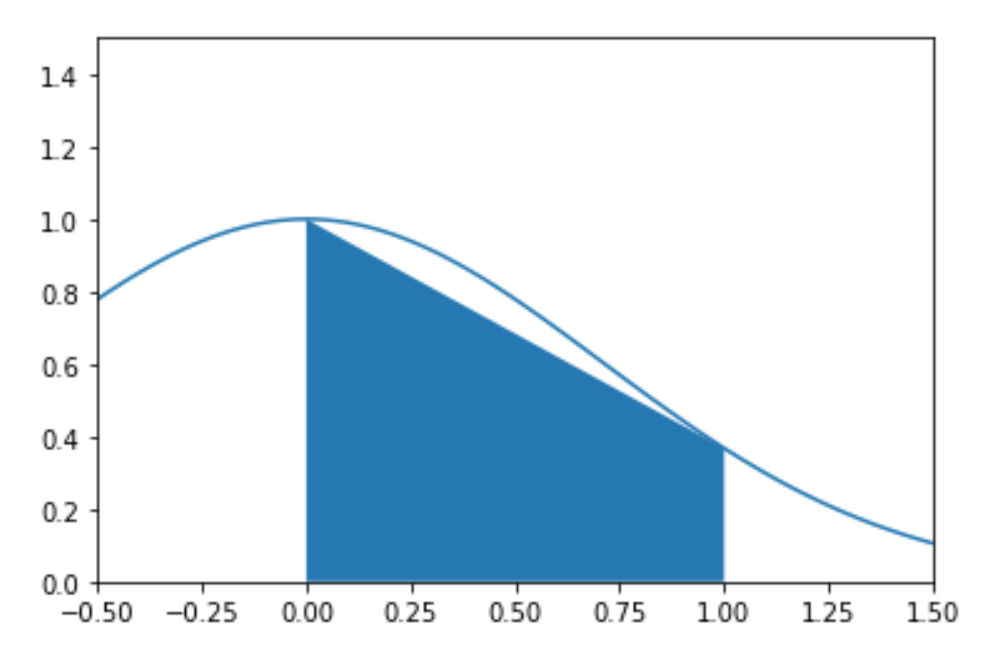
# https://www.math.ubc.ca/~pwalls/math-python/integration/trapezoid-rule/
import numpy as np
def my_trapz(f,a,b,N=50):
'''Approximate the integral of f(x) from a to b by the trapezoid rule.
The trapezoid rule approximates the integral \int_a^b f(x) dx by the sum:
(dx/2) \sum_{k=1}^N (f(x_k) + f(x_{k-1}))
where x_k = a + k*dx and dx = (b - a)/N.
Parameters
----------
f : function
Vectorized function of a single variable
a , b : numbers
Interval of integration [a,b]
N : integer
Number of subintervals of [a,b]
Returns
-------
float
Approximation of the integral of f(x) from a to b using the
trapezoid rule with N subintervals of equal length.
Examples
--------
>>> trapz(np.sin,0,np.pi/2,1000)
0.9999997943832332
'''
x = np.linspace(a,b,N+1) # N+1 points make N subintervals
y = f(x)
y_right = y[1:] # right endpoints
y_left = y[:-1] # left endpoints
dx = (b - a)/N
T = (dx/2) * np.sum(y_right + y_left)
return T
def vf(x):
return np.exp(np.cos(-2 * x * np.pi))
res1 = my_trapz(vf,-2,2)
print(f"The numerical result is {res1:f}")
from scipy.integrate import trapz
#help(trapz)
L'input di trapz sono l'array delle coordinate y e quello delle coordinate x in questo ordine.
x = np.linspace(-2,2,101)
y = vf(x)
res2 = trapz(y,x)
res2
Anche per simps l'input è costituito dall'array delle coordinate y e da quello delle coordinate x nell'ordine.
from scipy.integrate import simps
#help(trapz)
x = np.linspace(-2,2,101)
y = vf(x)
res2 = simps(y,x)
res2
Usando la funzione di scipy quad , scrivete un programmma che calcola numericamente il seguente integrale: $I = \int
_0^1\cos(2\pi x) dx$.
Calcolate analiticamente l'integrale (Potreste usare sympy) e confrontate i due risultati.
Perchè è importante avere una stima dell'accuratezza o errore dell'integrale numerico?
È bene fare il grafico della funzione integranda per controllarne il comportamento prima di cercare di integrarla. Singolarità (per esempio valori di $x$ in cui $f(x)$ tende a più o meno infinito) oppure altri comportamenti irregolari, come quello di $f(x)=\sin(\frac{1}{x}$) nell'intorno di $x = 0$, sono estremamente difficili e talvolta semplicemente impossibili da trattare numericamente.
plotquad che prende gli stessi argomenti del comando quad(cioè $f$, $a$ e $b$) e che quad, ritornando lo stesso set di valori di quad.
<\p>
<\p>
<\p>
<\p>
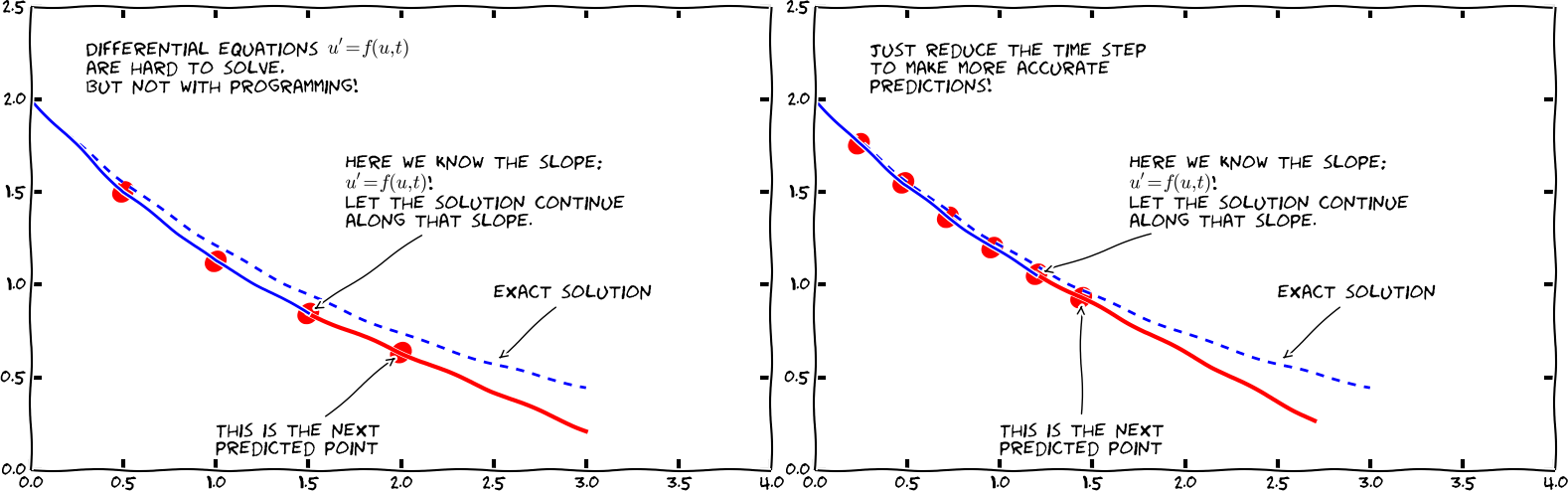 (Svein Linge, Hans Petter Langtangen - Programming for Computations)
(Svein Linge, Hans Petter Langtangen - Programming for Computations)
<\p>
<\p>
Per risolvere equazioni differenziali ordinarie del tipo $$\frac{\mathrm{d}y}{\mathrm{d}t}(t) = f(y,t)$$
con condizione iniziale $y(t_0)=y_0$, si può usare la funzione odeint di scipy. Ecco un esempio (useodeint.py) per determinare
data l'equazione differenziale: $$\frac{\mathrm{d}y}{\mathrm{d}t}(t) = -2yt \quad \mathrm{with} \quad y(0)=1.$$
from scipy.integrate import odeint
import numpy as np
def f(y, t):
"""this is the rhs of the ODE to integrate, i.e. dy/dt=f(y,t)"""
return -2 * y * t
y0 = 1 # initial value
a = 0 # integration limits for t
b = 2
t = np.arange(a, b, 0.01) # values of t for
# which we require
# the solution y(t)
y = odeint(f, y0, t) # actual computation of y(t)
import matplotlib.pyplot as plt # plotting of results
fig, ax = plt.subplots()
ax.plot(t,y)
ax.set_xlabel('t')
ax.set_ylabel('y(t)')
# https://www.math.ubc.ca/~pwalls/math-python/differential-equations/first-order/
def odeEuler(f,y0,t):
'''Approximate the solution of y'=f(y,t) by Euler's method.
Parameters
----------
f : function
Right-hand side of the differential equation y'=f(t,y), y(t_0)=y_0
y0 : number
Initial value y(t0)=y0 wher t0 is the entry at index 0 in the array t
t : array
1D NumPy array of t values where we approximate y values. Time step
at each iteration is given by t[n+1] - t[n].
Returns
-------
y : 1D NumPy array
Approximation y[n] of the solution y(t_n) computed by Euler's method.
'''
y = np.zeros(len(t))
y[0] = y0
for n in range(0,len(t)-1):
y[n+1] = y[n] + f(y[n],t[n])*(t[n+1] - t[n])
return y
y_E = odeEuler(f,y0,t)
import matplotlib.pyplot as plt # plotting of results
fig, ax = plt.subplots()
ax.plot(t,y,label='sol by odeint')
ax.plot(t,y_E,c='r',label='sol by odeEuler')
ax.set_xlabel('t')
ax.set_ylabel('y(t)')
ax.legend()
Il comando odeint può prendere diversi parametri opzionali per modificare l'errore di default nell'integrazione (e per produrre output addizionale che può essere utile per il debugging). Usate il comando help per farvene un'idea:
help(scipy.integrate.odeint)
restituisce:
Help on function odeint in module scipy.integrate.odepack:
odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0)
Integrate a system of ordinary differential equations.
Solve a system of ordinary differential equations using lsoda from the
FORTRAN library odepack.
Solves the initial value problem for stiff or non-stiff systems
of first order ode-s::
dy/dt = func(y, t0, ...)
where y can be a vector.
*Note*: The first two arguments of ``func(y, t0, ...)`` are in the
opposite order of the arguments in the system definition function used
by the `scipy.integrate.ode` class.
Parameters
----------
func : callable(y, t0, ...)
Computes the derivative of y at t0.
y0 : array
Initial condition on y (can be a vector).
t : array
A sequence of time points for which to solve for y. The initial
value point should be the first element of this sequence.
args : tuple, optional
Extra arguments to pass to function.
Dfun : callable(y, t0, ...)
Gradient (Jacobian) of `func`.
col_deriv : bool, optional
True if `Dfun` defines derivatives down columns (faster),
otherwise `Dfun` should define derivatives across rows.
full_output : bool, optional
True if to return a dictionary of optional outputs as the second output
printmessg : bool, optional
Whether to print the convergence message
Returns
-------
y : array, shape (len(t), len(y0))
Array containing the value of y for each desired time in t,
with the initial value `y0` in the first row.
infodict : dict, only returned if full_output == True
Dictionary containing additional output information
======= ============================================================
key meaning
======= ============================================================
'hu' vector of step sizes successfully used for each time step.
'tcur' vector with the value of t reached for each time step.
(will always be at least as large as the input times).
'tolsf' vector of tolerance scale factors, greater than 1.0,
computed when a request for too much accuracy was detected.
'tsw' value of t at the time of the last method switch
(given for each time step)
'nst' cumulative number of time steps
'nfe' cumulative number of function evaluations for each time step
'nje' cumulative number of jacobian evaluations for each time step
'nqu' a vector of method orders for each successful step.
'imxer' index of the component of largest magnitude in the
weighted local error vector (e / ewt) on an error return, -1
otherwise.
'lenrw' the length of the double work array required.
'leniw' the length of integer work array required.
'mused' a vector of method indicators for each successful time step:
1: adams (nonstiff), 2: bdf (stiff)
======= ============================================================
Other Parameters
----------------
ml, mu : int, optional
If either of these are not None or non-negative, then the
Jacobian is assumed to be banded. These give the number of
lower and upper non-zero diagonals in this banded matrix.
For the banded case, `Dfun` should return a matrix whose
rows contain the non-zero bands (starting with the lowest diagonal).
Thus, the return matrix `jac` from `Dfun` should have shape
``(ml + mu + 1, len(y0))`` when ``ml >=0`` or ``mu >=0``.
The data in `jac` must be stored such that ``jac[i - j + mu, j]``
holds the derivative of the `i`th equation with respect to the `j`th
state variable. If `col_deriv` is True, the transpose of this
`jac` must be returned.
rtol, atol : float, optional
The input parameters `rtol` and `atol` determine the error
control performed by the solver. The solver will control the
vector, e, of estimated local errors in y, according to an
inequality of the form ``max-norm of (e / ewt) <= 1``,
where ewt is a vector of positive error weights computed as
``ewt = rtol * abs(y) + atol``.
rtol and atol can be either vectors the same length as y or scalars.
Defaults to 1.49012e-8.
tcrit : ndarray, optional
Vector of critical points (e.g. singularities) where integration
care should be taken.
h0 : float, (0: solver-determined), optional
The step size to be attempted on the first step.
hmax : float, (0: solver-determined), optional
The maximum absolute step size allowed.
hmin : float, (0: solver-determined), optional
The minimum absolute step size allowed.
ixpr : bool, optional
Whether to generate extra printing at method switches.
mxstep : int, (0: solver-determined), optional
Maximum number of (internally defined) steps allowed for each
integration point in t.
mxhnil : int, (0: solver-determined), optional
Maximum number of messages printed.
mxordn : int, (0: solver-determined), optional
Maximum order to be allowed for the non-stiff (Adams) method.
mxords : int, (0: solver-determined), optional
Maximum order to be allowed for the stiff (BDF) method.
See Also
--------
ode : a more object-oriented integrator based on VODE.
quad : for finding the area under a curve.
Examples
--------
The second order differential equation for the angle `theta` of a
pendulum acted on by gravity with friction can be written::
theta''(t) + b*theta'(t) + c*sin(theta(t)) = 0
where `b` and `c` are positive constants, and a prime (') denotes a
derivative. To solve this equation with `odeint`, we must first convert
it to a system of first order equations. By defining the angular
velocity ``omega(t) = theta'(t)``, we obtain the system::
theta'(t) = omega(t)
omega'(t) = -b*omega(t) - c*sin(theta(t))
Let `y` be the vector [`theta`, `omega`]. We implement this system
in python as:
>>> def pend(y, t, b, c):
... theta, omega = y
... dydt = [omega, -b*omega - c*np.sin(theta)]
... return dydt
...
We assume the constants are `b` = 0.25 and `c` = 5.0:
>>> b = 0.25
>>> c = 5.0
For initial conditions, we assume the pendulum is nearly vertical
with `theta(0)` = `pi` - 0.1, and it initially at rest, so
`omega(0)` = 0. Then the vector of initial conditions is
>>> y0 = [np.pi - 0.1, 0.0]
We generate a solution 101 evenly spaced samples in the interval
0 <= `t` <= 10. So our array of times is:
>>> t = np.linspace(0, 10, 101)
Call `odeint` to generate the solution. To pass the parameters
`b` and `c` to `pend`, we give them to `odeint` using the `args`
argument.
>>> from scipy.integrate import odeint
>>> sol = odeint(pend, y0, t, args=(b, c))
The solution is an array with shape (101, 2). The first column
is `theta(t)`, and the second is `omega(t)`. The following code
plots both components.
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, sol[:, 0], 'b', label='theta(t)')
>>> plt.plot(t, sol[:, 1], 'g', label='omega(t)')
>>> plt.legend(loc='best')
>>> plt.xlabel('t')
>>> plt.grid()
>>> plt.show()odeint¶Aprite un nuovo file chiamato testodeint.py con un text editor.
Scrivete un programma che calcola la soluzione y(t) della ODE seguente, usando l'algoritmo odeint,
$$\frac{\mathrm{d}y}{\mathrm{d}t} = -\exp(-t)(10\sin(10t)+\cos(10t))$$
da $t=0$ a $t = 10$. Il valore iniziale è $y(0)=1$.
Mostrate graficamente la soluzione, valutandola nei punti $t=0$, $t=0.01$, $t=0.02$, ..., $t=9.99$, $t=10$.
Aiutino: una parte della soluzione $y(t)$ è presentata nella figura seguente.
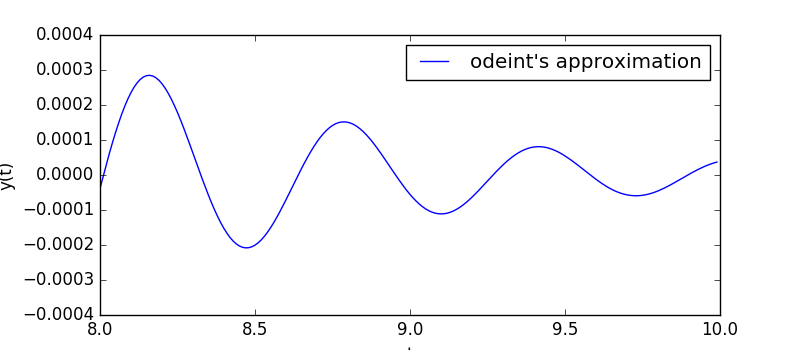
<\p>
<\p>
Cercare una $x$ tale che $$f(x)=0$$ si chiama ricerca delle radici. Si noti che un problema del tipo $g(x)=h(x)$ può essere riformulato come $f(x)=g(x)−h(x)=0$.
Il modulo optimize di scipy fornisce diversi strumenti per la ricerca delle radici.
<\p>
<\p>
 (Svein Linge, Hans Petter Langtangen - Programming for Computations)
(Svein Linge, Hans Petter Langtangen - Programming for Computations)
<\p>
<\p>
L'algoritmo bisect è (i) robusto e (ii) concettualmente molto semplice (ma lento).
Supponiamo di dover calcolare le radici di $f(x)= x^3 − 2 x^2$. Questa funzione ha una radice (doppia) in $x = 0$ e un'altra fra $x = 1.5$ (dove $f(1.5) = − 1.125$) e $x = 3$ (dove $f(3) = 9$). È facile vedere che questa altra radice si trova in $x = 2$. Ecco il programma che determina la radice numericamente:
from scipy.optimize import bisect
def f(x):
"""returns f(x)=x^3-2x^2. Has roots at
x=0 (double root) and x=2"""
return x ** 3 - 2 * x ** 2
# main program starts here
x = bisect(f, 1.5, 3, xtol=1e-6)
print(f"The root x is approximately x={x:14.12g},\n"
f"the error is less than 1e-6.")
print(f"The exact error is {2 - x:g}.")
Il metodo bisect() richiede obbligatoriamente tre argomenti: (i) la funzione f(x), (ii) il limite inferiore a (che abbiamo scelto uguale a 1.5 nell'esempio) e (ii) il limite superiore b (scelto uguale a 3). Il parametro opzionale xtol determina l'errore massimo del metodo.
Uno dei presupposti del metodo di bisezione è che l'intervallo [a, b] sia scelto in modo tale che la funzione abbia in a segno opposto a quello che ha in b in modo che nell'intervallo, se la funzione è continua, cada almeno una radice.
Scrivete un programma chiamato sqrttwo.py per determinare un valore approssimato di $\sqrt{2}$ cercando la radice x della funzione $f(x)=2 − x^2$ usando il metodo di bisezione. Scegliete come tolleranza per l'approssimazione alla radice di 10−8.
Documentate la scelta dell'intervallo iniziale $[a, b]$ per la ricerca: che valori evte scelto per a e b? Perchè?
Esaminate i risultati:
Che valore restituisce l'algoritmo di bisezione per la radice x?
Calcolate il valore di $\sqrt{2}$ usando math.sqrt(2) e confrontatelo il risultato precedente. Quanto è grande l'errore assoluto? Come si confronta con xtol?
Morale della favola: mai accettare il risultato di una routine numerica senza esaminarlo con attenzione e per quanto possibile verificarlo.
fsolve¶Un algoritmo per la ricerca delle radici che è (spesso) migliore (nel senso di “più efficiente”) di quello di bisezione è codificato nella funzione fsolve() che funziona anche per problemi a più dimensioni. Questo algoritmo richiede solamente un punto di partenza vicino a dove ci si aspetta che ci sia una radice (Non è però detto che il metodo converga).
Ecco un esempio:
from scipy.optimize import fsolve
def f(x):
return x ** 3 - 2 * x ** 2
xstart = 3
x = fsolve(f, xstart) # one root is at x=2.0
# search starts at x=3
# fsolve returns a numpy array
print(f"The root x is approximately x={x[0]:21.19g}")
print(f"The exact error is {2 - x[0]:g}.")
Il valore restituito da fsolve è un array di numpy di lunghezza $n$ per un problema di ricerca di radici con $n$ variabili. Nell'esempio precedente, $n = 1$.
Scipy fornisce una funzione piuttosto flessibile (basato sull'algoritmo di Levenburg-Marquardt), scipy.optimize.curve_fit, per interpolare un set di dati. L'assunzione è che vengano dati un set di punti
$x_1, x_2,\cdots,x_N$, i corrispondenti valori $y_i$ e una dipendenza funzionale $y=f(x,\vec{p})$.
Per fare un esempio, il numero di atomi non decaduti in un campione di una sostanza radioattiva segue la legge
$$ N(t,N_0,\tau) = N_0\,\exp\left(-\frac{t}{\tau}\right).$$
Si vuole determinare i parametri $\vec{p}=(p_1, p_2, \ldots,p_k)$ in modo che $r$, la somma degli scarti quadratici fra la curva e i dati, sia la più piccola possibile:
Questo approccio è particolarmente utile quando i dati sono affetti da rumore: per ogni coppia $x_i,y_i$ è presente un termine di errore (ignoto) $\epsilon_i$, tale che $y_i=f(x_i,\vec{p})+\epsilon_i$.
Un esempio per chiarire: assumiamo di avere dei dati che sappiamo essere descritti dalla funzione: $$f(x,\vec{p}) = a \exp(-b x) + c,$$ che dipende dai parametri $\vec{p}=(a,b,c)$, che devono essere determinati usando i dati.
import numpy as np
from scipy.optimize import curve_fit
def f(x, a, b, c):
"""Fit function y=f(x,p) with parameters p=(a,b,c). """
return a * np.exp(- b * x) + c
#create fake data
x = np.linspace(0, 4, 50)
y = f(x, a=2.5, b=1.3, c=0.5)
#add noise
yi = y + 0.2 * np.random.normal(size=len(x))
#call curve fit function
popt, pcov = curve_fit(f, x, yi)
# extract fit parameters
af, bf, cf = popt
print(f"Optimal parameters are af={af:g}, bf={bf:g}, and cf={cf:g}.")
# best fit curve
yfitted = f(x,af,bf,cf)
#plot
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(6,4))
ax.scatter(x, yi, marker='o', label='data $y_i$')
ax.plot(x, yfitted, c='r', label='fit $f(x_i)$')
ax.set_xlabel('x')
ax.legend()
Si noti che nell'esempio precedente abbiamo definito la funzione da utilizzare per il fit y = f(x)$ usando del codice Python. Quindi possiamo utilizzare una funzione (quasi) arbitraria nel metodo curve_fit.
La funzione curve_fit restituisce una tuple popt, pcov. Il primo elemento, popt, contiene l'ntupla dei parametri ottimali (OPTimal Parameters), cioè i parametri che minimizzano la somma degli scarti quadratici. Il secondo elemento contiene la matrice di covarianza di tutti i parametri (Sperimentazioni di Fisica). La diagonale fornisce la varianza della stima dei parametri.
L'algoritmo di Levenburg-Marquardt richiede, per iniziare la sua procedura, una stima iniziale dei parametri. Se questa non viene fornita, come nell'esempio precedente, il valore “1.0“ viene assunto come stima di partenza.
Se l'algoritmo non riesce a fittare i dati con la funzione ipotizzata, è necessario fornire a curve_fit una stima migliore per i parametri iniziali. Nell'esempio precedente potremmo passare le nostre stime cambiando la linea
popt, pcov = curve_fit(f, x, yi)
in
popt, pcov = curve_fit(f, x, yi, p0=(2,1,0.6))
se avessimo ragione di ritenere che a = 2, b = 1 and c = 0.6 siano dei valori "ragionevoli". Una volta che la stima iniziale è "più o meno corretta" il fit funziona bene.
Spesso è necessario trovare il massimo o il minimo di una particolare funzione f(x) dove f è una funzione scalare mentre x può essere un vettore. Applicazioni tipiche sono la minimizzazione di quantità come il costo, il rischio o l'errore, oppure la massimizzazione della produttività, efficienza o profitto. Le routines di ottimizzazione tipicamente forniscono un metodo per minimizzare una funzione data: per massimizzare f(x) è sufficiente minimizzare g(x)= − f(x).
Di seguito, un esempio che mostra (i) the definizione din funzione di test function e (ii) la chiamata a scipy.optimize.fmin a cui vengono passati la funzione f da minimizzare e un valore iniziale x0 da cui partire per la ricerca del minimo, e che restituisce il valore x per cui f(x) ha un minimo locale. Tipicamente, la ricerca del minimo è locale, nel senso che l'algoritmo segue il gradiente (derivata multidimensionale) nel punto in cui si trova. Cerchiamo il minimo partendo da due punti diversi (x0 = 1.0 e x0 = 2.0, respectively) per dimostrare che, a seconda del punto di partenza, possiamo trovare minimi diversi della funzione f.
La maggior parte dei comandi, dopo le due chiamate a fmin, generano il plot della funzione, mostrando i punti iniziali delle due ricerche e i minimi ottenuti:
import numpy as np
from scipy.optimize import fmin
import matplotlib.pyplot as plt
def f(x):
return np.cos(x) - 3 * np.exp( -(x - 0.2) ** 2)
# find minima of f(x),
# starting from 1.0 and 2.0 respectively
minimum1 = fmin(f, 1.0)
print("Start search at x=1., minimum is", minimum1)
minimum2 = fmin(f, 2.0)
print("Start search at x=2., minimum is", minimum2)
# plot function
x = np.arange(-10, 10, 0.1)
y = f(x)
fig, ax = plt.subplots(figsize=(6,4))
ax.set_xlabel('x')
ax.grid(b=True,which='both')
ax.set_xlim(-5.,5.)
ax.set_ylim(-2.2,0.5)
ax.plot(x, y, label='$\cos(x)-3e^{-(x-0.2)^2}$')
# add minimum1 to plot
ax.scatter(minimum1, f(minimum1), marker='v', c='r', label='minimum 1')
# add start1 to plot
ax.scatter(1.0, f(1.0), marker='o', c='r', label='start 1')
# add minimum2 to plot
ax.scatter(minimum2,f(minimum2), marker='v', c='g', label='minimum 2')
# add start2 to plot
ax.scatter(2.0,f(2.0), marker='o', c='g',label='start 2')
ax.legend(loc='lower left')
Come si vede, la chiamata a fmin produce anche dell'output addizionale che può essere utile per analizzare la procedura.
fmin¶Si noti che la funzione fmin restituisce un numpy array che – nel caso precedente – contiene un solo numero dal momento che abbiamo una sola variabile (qui x) da variare. In generale, fmin può essre usata per trovare il minimo in uno spazio pluridimensionale. In questo caso, il numpy array contiene le coordinate del punto che minimizza la funzione obiettivo.
Scientific Python and Numpy forniscono molti altri algoritmi numerici: per esempio interpolazione di funzioni, trasformate di Fourier, ottimizzazione, funzioni speciali (Funzioni di Bessel etc.), generazione di numeri casuali, signal processing e filtri.
Ulteriori informazioni ed esempi: Scipy-lectures.