11: Metodo Monte Carlo

Introduzione

Il Metodo Monte Carlo si riferisce a un insieme di tecniche di calcolo e simulazione che si basano sull'uso di numeri casuali.

11.1 Integrazione numerica con metodo MC

L'idea di usare numeri casuali per calcolare un integrale numerico si basa sul teorema della media in Analisi che afferma che l'integrale $\int_a^b f(x)\,dx$ è uguale al prodotto della lunghezza (con segno) dell'intervallo di integrazione $(b-a)$ per il valor medio della funzione $f$, $<f>$, nell'intervallo. Il valor medio può essere calcolato facendo la media dei valori di $f$ in un set di punti scelti a caso in $[a,b]$.
Esempio: $\int_1^2 x^2 dx = \frac{7}{3}$

import numpy as np

npoints=10
xval=np.random.random(npoints)+1.   #punti casuali in [1,2]
#print(xval)

y_ave=np.mean(xval*xval)
my_int=y_ave*(2.-1.)
print("Stima dell'integrale:",my_int)
print("Risultato esatto:",7/3)

Stima dell'integrale: 2.1106972670426414
Risultato esatto: 2.3333333333333335

Confrontate il risultato con quello fornito dal metodo dei trapezi e da quad nel notebook 10_scipy.

Esempio in più dimensioni: il volume di una semisfera di raggio 1: $$\int_{-1}^1 dx \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}dy\,\sqrt{1-x^2-y^2} = \frac{2}{3}\pi$$

npoints = 100
xval=2*np.random.random(npoints)-1.
#print(xval)
yval=2*np.random.random(npoints)-1.
#print(yval)
points=[pair for pair in zip(xval,yval) if pair[0]**2 + pair[1]**2 < 1.] #zip returns tuples
points=np.array(points)
#type(points)
#len(points)
#print(points)

def my_f(point):
    return np.sqrt(1.- (point*point).sum(axis=1)).mean()

base_area=np.pi
print("Stima dell'integrale:",base_area*my_f(points))
print("Risultato esatto:",2/3*np.pi)

Stima dell'integrale: 2.094625867312567
Risultato esatto: 2.0943951023931953

Il grande vantaggio del metodo Monte Carlo è che si può estendere immediatamente a qualunque numero di dimensioni.

11.2 Generazione di eventi distribuiti secondo una densità di probabilità fissata

Metodo hit and miss

Supponiamo di avere la seguente distribuzione di probabilità: $$P(x) = \begin{cases} 0.6 \quad x<0.5\\ 1.7 \quad x>0.5 \end{cases}$$

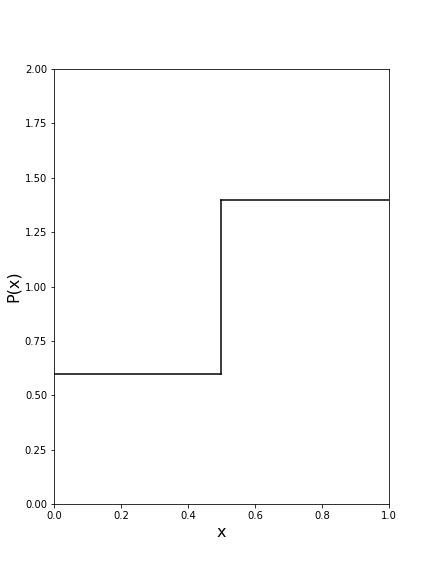
e di voler generare valori di $x$ distribuiti secondo $P(x)$

Procediamo nel modo seguente:

• Troviamo un numero $Y$ tale che $P(x) < Y, \,\forall x$. Nel nostro caso potremmo prendere $Y = 2$, per esempio.
• Generiamo un numero casuale $x_0$ in [0,1], in modo uniforme.
• Generiamo un secondo numero casuale $y_0$ in [0,$Y$]
• Teniamo il numero $x_0$ nel sample se $y_0 < P(x_0)$ altrimenti lo scartiamo e generiamo un nuovo valore $x_0$.

La probabilità di tenere un punto nel bin di sinistra è: $$P_{sx}=P(x < 0.5)\cdot P(y < 0.6) = 0.5\cdot\frac{0.6}{2}$$ La probabilità di tenere un punto nel bin di destra è: $$P_{dx}=P(x > 0.5)\cdot P(y < 1.7) = 0.5\cdot\frac{1.4}{2}$$ Quindi il rapporto $R$ fra le due probabilità, ovvero il rapporto fra il numero di punti accettati in $x < 0.5$ e il numero di punti accettati in $x > 0.5$ è, come deve: $$ R = \frac{P_{sx}}{P_{dx}} = \frac{0.6}{1.7}$$

npoints=1000
# npoints = 1000000
xval=np.random.random(npoints)
# Separo i valori minori/maggiori di 0.5
x1val=[x for x in xval if x < 0.5]
x2val=[x for x in xval if x > 0.5]

y1=0.6
y2=1.4

x1val=[x for x in x1val if y1 > np.random.random()*2]
x2val=[x for x in x2val if y2 > np.random.random()*2]

print("Numero di punti in [0,0.5]:",len(x1val))
print("Numero di punti in [0.5,1]:",len(x2val))
print("rapporto fra i numeri di punti:",len(x2val)/len(x1val),"rapporto atteso=7/3:",7/3)

Numero di punti in [0,0.5]: 135
Numero di punti in [0.5,1]: 381
rapporto fra i numeri di punti: 2.8222222222222224 rapporto atteso=7/3: 2.3333333333333335

Test della generazione Monte Carlo di punti secondo una distribuzione data

Una funzione generica per generare eventi secondo una distribuzione qualsiasi

import numpy as np

def generate_f(f,a,b,max):
    '''
    Generate random points distributed according to an input distribution
    Input:
    f: the probability distribution
    a,b: extrema of the range for the desired random number
    max: a real number such that f(x) < max for each x
    Returns:
    ranval: random number
    '''
    not_found=True
    while not_found:
        x=np.random.uniform(a,b)
        y=np.random.uniform(0,max)
        if f(x)>y:
            not_found=False
    
    return x
    

Esempio 1

def f1(x):
    if x < 0.5:
        val=0.6
    else:
        val=1.4
    
    return val
    

#npoints=1000
npoints = 1000000
xval = [generate_f(f1,0,1,2) for n in range(npoints)]
x1val=[x for x in xval if x < 0.5]
x2val=[x for x in xval if x > 0.5]

print("Numero di punti in [0,0.5]:",len(x1val))
print("Numero di punti in [0.5,1]:",len(x2val))
print("rapporto fra i numeri di punti:",len(x2val)/len(x1val),"rapporto atteso=7/3:",7/3)

Numero di punti in [0,0.5]: 299487
Numero di punti in [0.5,1]: 700513
rapporto fra i numeri di punti: 2.3390430970292533 rapporto atteso=7/3: 2.3333333333333335

import matplotlib.pyplot as plt
nbins = 10
xrange = (0,1)

fig, ax = plt.subplots()
nevent, bins, patches = ax.hist(xval, nbins, range=xrange)

Esempio 2

def f2(x):
    val=3./8.*(1+x**2)
    
    return val    

#npoints=1000
npoints = 100000
xval = [generate_f(f2,-1,1,1) for n in range(npoints)]

nbins = 20
xrange = (-1,1)

fig, ax = plt.subplots(figsize=(10,7))
nevent, bins, patches = ax.hist(xval, nbins, range=xrange)
ax.grid(True)

11.3 Propagazione dell'errore con metodo MC

Supponiamo di aver fatto un esperimento per misurare l'accelerazione di gravità $g$ misurando il periodo $T$ di oscillazione di un pendolo di lunghezza variabile $L$. Sappiamo che: $$ T = 2 \pi \sqrt{\frac{L}{g}} \quad \rightarrow \quad g = \frac{ 4 \pi^2 L}{T^2}$$ Supponiamo di aver misurato $L = 1.000 \pm 0.004\, m$, $T = 2.000 \pm 0.005\, s$ e che le misure siano distribuite gaussianamente. Per la propagazine degli errori ci servono: $$ \frac{\partial g}{\partial T} = \frac{ - 8 \pi^2 L}{T^3},\qquad \frac{\partial g}{\partial L} = \frac{ 4 \pi^2}{T^2}$$

$$ \sigma_g = \sqrt{\left. \sigma_T \, \frac{\partial g}{\partial T}\right|^2_{\overline{T},\overline{L}} + \left. \sigma_L \, \frac{\partial g}{\partial L}\right|^2_{\overline{T},\overline{L}} }$$

import numpy as np
import matplotlib.pyplot as plt

def g(L,T):
    return 4*np.pi**2*L/T**2

def g_err(L,L_err,T,T_err):
    return 4*np.pi**2/T**2*np.sqrt(4*(L/T*T_err)**2 + L_err**2)

L_mean =1.0
L_err = 0.004
T_mean = 2.0
T_err = 0.005

g_m = g(L_mean,T_mean)
g_e = g_err(L_mean,L_err,T_mean,T_err)
print(f"g_exp = {g_m} +\- {g_e}")

g_exp = 9.869604401089358 +\- 0.06319630315448918

Per valutare l'errore su $g$ con il metodo Monte Carlo generiamo 1000 valori per L e 1000 per T da distribuzioni gaussiane con i rispettivi valori medi e deviazioni standard. Calcoliamo i corrispondenti valori di $g$ e valutiamo il valor medio e la deviazione standard della distribuzione ottenuta.

npoints = 1000
T_test = np.random.normal(T_mean,T_err,npoints)
L_test = np.random.normal(L_mean,L_err,npoints)
g_test = g(L_test,T_test)
g_m1 = g_test.mean()
g_e1 = g_test.std()
print(f"g_MC = {g_m1} +\- {g_e1}")

g_MC = 9.869774050229458 +\- 0.06177237499636006

Plot di controllo

Nota sulle normalizzazioni:

- Dato un istogramma con $N_{tot}$ valori, i valori in ciascun bin sommano a $N_{tot}$.    
- Se si vuole sovrapporre una gaussiana $g(x)$ all'istogramma bisogna ricordare che: $\int g(x)\,dx = \sum_i g(x_i) w =1$, dove $w$ è la larghezza di ciascun bin. Di conseguenza i valori di $g(x)$ vanno moltiplicati per $w \cdot N_{tot}$ per avere un confronto significativo.

def Gauss_dist(t,lam,sigma):
    return np.exp(-0.5*((t-lam)/sigma)**2)/np.sqrt(2*np.pi)/sigma

fig1, ax1 = plt.subplots()

nbins = 20
range1 = (L_mean - 3*L_err,L_mean + 3*L_err)
ax1.hist(L_test,nbins,range1,color='b',label='L');

fig2, ax2 = plt.subplots()

nbins = 20
range2 = (T_mean - 3*T_err,T_mean + 3*T_err)
ax2.hist(T_test,nbins,range2,color='r',label='T');


fig3, ax3 = plt.subplots()

nbins = 20
range3 = (g_m1 - 3*g_e1,g_m1 + 3*g_e1)
binwidth = 6*g_e1/nbins

ax3.hist(g_test,nbins,range3,color='g',label='g');

t = np.linspace(g_m1 - 3*g_e1,g_m1 + 3*g_e1,100)
yval = Gauss_dist(t,g_m1,g_e1)*npoints*binwidth
#yval = np.array([np.exp(-0.5*((t1-g_m1)/g_e1)**2)/np.sqrt(2*np.pi)/g_e1 for t1 in t])
#print(yval)

ax3.plot(t,yval,c='k')

[<matplotlib.lines.Line2D at 0x120ed7e10>]

11.4 Simulazione di eventi complessi con metodo MC