Un esempio di algoritmo

Il problema

Dato $q$, trovare $r >0$, tale che $r\, = \, \sqrt{q}$, con un errore più piccolo di $\epsilon$.

Il procedimento

Se $r = \sqrt{q}$ allora $r \cdot r = q$.

  • Partiamo da un valore stimato $g$.
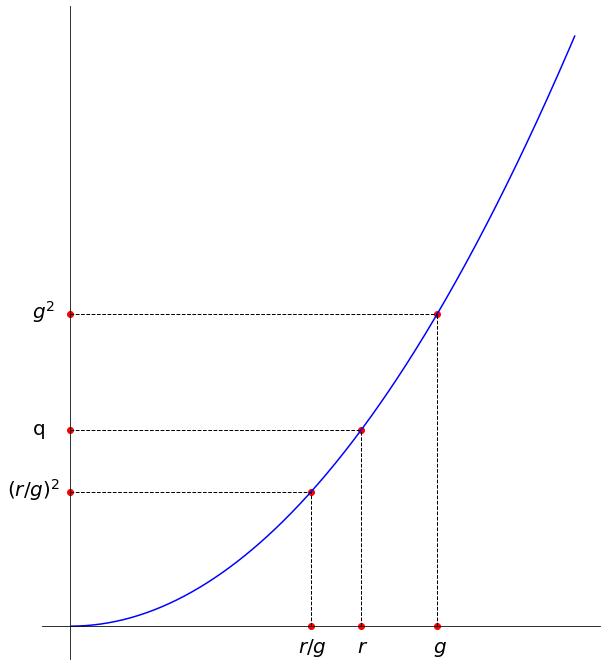
  • Se $g^2 > q$ allora $g > r$. Inoltre $r = q/r > q/g$. Quindi $g > r > q/g$. (Controllate cosa succede se $g^2 < q$.)
  • Se $\vert g\cdot g - q \vert < \epsilon$ accettiamo $g$ come risposta. Altrimenti prendiamo come nuova stima per $g$ il punto medio fra $g$ e $q/g$, $g_1 = 1/2 \cdot (g + q/g)$.
  • Ripetiamo finchè la stima finale $g_f$ è tale che $\vert g_f \cdot g_f - q \vert < \epsilon$

In [1]:
def mysqrt(q,g,epsilon):            # I tre argomenti devono essere passati tutti.
    while(abs(g*g - q) > epsilon):
        g = (g + q/g)/2.
    return g
In [2]:
mysqrt(16.,3)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-2-a2450e0411af> in <module>
----> 1 mysqrt(16.,3)

TypeError: mysqrt() missing 1 required positional argument: 'epsilon'
In [8]:
mysqrt(16.,3.,1.e-7)
Out[8]:
4.000000000000241
In [3]:
def mysqrt2(q,g,epsilon=1.e-5):   # L'argomento epsilon è opzionale. Se non viene passato, assume il valore 1.e-5
    while(abs(g*g - q) > epsilon):
        g = (g + q/g)/2.
    return g
In [4]:
mysqrt2(16.,6.)
Out[4]:
4.000000000052429
In [16]:
mysqrt2(16.,6.,1.e-3)
Out[16]:
4.000020480052429
In [5]:
mysqrt2(16.,6.,1.e-15)
Out[5]:
4.0

Il nostro algoritmo ha:

  • un punto di partenza (fornito dall'utente)
  • una sequenza definita di operazioni
  • un criterio per interrompere il procedimento
In [ ]: