



Next: Conservation laws
Up: Two-dimensional turbulence
Previous: Two-dimensional turbulence
Contents
In two dimensions, the incompressible velocity field
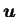 can be expressed in terms of the stream-function
can be expressed in terms of the stream-function 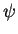 as:
as:
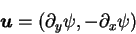 |
(1.58) |
The vorticity field, defined as the curl of velocity,
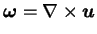 , in two dimensions has
only one non-zero component which is orthogonal to the plane of velocity
and is related to the stream-function by
, in two dimensions has
only one non-zero component which is orthogonal to the plane of velocity
and is related to the stream-function by
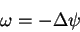 |
(1.59) |
Thus instead of giving a description of the flow in term of the
two components of velocity, which are not independent because
of the incompressibility condition, it is convenient to rewrite
the two-dimensional Navier-Stokes equations
in terms of the vorticity scalar field:
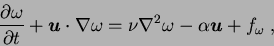 |
(1.60) |
The linear dissipative term accounts
for friction between the thin layer of fluid which is considered,
and the rest of the three dimensional environment.
Its effects will be discussed in the following chapter.
The term 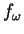 represents the external source of energy acting on the
largest scales - e.g. stirring. This term counteracts the dissipation
by viscosity
represents the external source of energy acting on the
largest scales - e.g. stirring. This term counteracts the dissipation
by viscosity 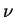 and friction
and friction 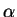 and allows to obtain a
statistically steady state.
and allows to obtain a
statistically steady state.
To solve Eq. (1.60) it is necessary to specify a set
of boundary conditions which are required to solve
the Poisson equation (1.59) for the stream function.
In most studies on 2D turbulence,
periodic boundary conditions are assumed in both the two directions.
The presence of realistic no-slip boundaries gives origin to a source
of vorticity fluctuations.




Next: Conservation laws
Up: Two-dimensional turbulence
Previous: Two-dimensional turbulence
Contents
Stefano Musacchio
2004-01-09
![]() can be expressed in terms of the stream-function
can be expressed in terms of the stream-function ![]() as:
as: