



Next: Passive polymers
Up: Two-dimensional turbulence of dilute
Previous: Two-dimensional turbulence of dilute
Contents
2D Oldroyd-B model
The study of two-dimensional viscoelastic solutions
will be addressed by means of the two-dimensional version of
Oldroyd-B model (3.12-3.16), which is
described by the equations:
The matrix
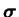 is the conformation tensor of polymer molecules
is the conformation tensor of polymer molecules
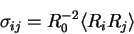 |
(4.3) |
and its trace
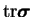 is a measure of their square
elongation. Because of its physical meaning the conformation tensor is
symmetric and positive definite.
The parameter
is a measure of their square
elongation. Because of its physical meaning the conformation tensor is
symmetric and positive definite.
The parameter 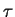 is the (slowest) polymer relaxation time toward the
equilibrium length
is the (slowest) polymer relaxation time toward the
equilibrium length 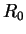 , therefore in absence of stretching the
conformation tensor therefore relaxes to the the unit tensor
, therefore in absence of stretching the
conformation tensor therefore relaxes to the the unit tensor
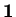 .
The matrix of velocity gradients which stretches the polymers is defined as
.
The matrix of velocity gradients which stretches the polymers is defined as
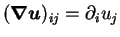 .
The solvent viscosity is denoted by
.
The solvent viscosity is denoted by 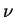 and
and
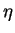 is the zero-shear contribution of polymers to the total solution
viscosity
is the zero-shear contribution of polymers to the total solution
viscosity
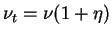 .
The pressure term
.
The pressure term
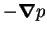 ensures incompressibility of the
velocity field, which can be expressed in terms of the stream-function
ensures incompressibility of the
velocity field, which can be expressed in terms of the stream-function 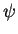 as
as
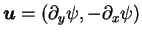 .
The dissipative term
.
The dissipative term
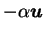 models the
mechanical friction between the thin layer of fluid and
the surrounding environment,
and plays a prominent role in the energy budget
of Newtonian two-dimensional turbulence [71].
The energy source is provided by the large-scale forcing
models the
mechanical friction between the thin layer of fluid and
the surrounding environment,
and plays a prominent role in the energy budget
of Newtonian two-dimensional turbulence [71].
The energy source is provided by the large-scale forcing
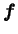 ,
which is Gaussian, statistically homogeneous and isotropic,
,
which is Gaussian, statistically homogeneous and isotropic,
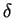 -correlated in time, with correlation length
-correlated in time, with correlation length 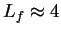 .
.
The numerical integration is performed by a fully dealiased
pseudospectral code, with second-order Runge Kutta scheme,
at different resolutions,
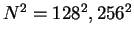 grid points,
on a doubly periodic square box of size
grid points,
on a doubly periodic square box of size 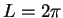 .
As customary, an artificial stress-diffusivity term
.
As customary, an artificial stress-diffusivity term
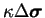 is added
to Eq.(4.2) to prevent numerical
instabilities [72].
For the passive case we have adopted a Lagrangian code
which explicitly which preserves the symmetries of the conformation tensor
(see Appendix A).
is added
to Eq.(4.2) to prevent numerical
instabilities [72].
For the passive case we have adopted a Lagrangian code
which explicitly which preserves the symmetries of the conformation tensor
(see Appendix A).




Next: Passive polymers
Up: Two-dimensional turbulence of dilute
Previous: Two-dimensional turbulence of dilute
Contents
Stefano Musacchio
2004-01-09
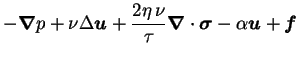
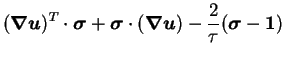
![]() grid points,
on a doubly periodic square box of size
grid points,
on a doubly periodic square box of size ![]() .
As customary, an artificial stress-diffusivity term
.
As customary, an artificial stress-diffusivity term
![]() is added
to Eq.(4.2) to prevent numerical
instabilities [72].
For the passive case we have adopted a Lagrangian code
which explicitly which preserves the symmetries of the conformation tensor
(see Appendix A).
is added
to Eq.(4.2) to prevent numerical
instabilities [72].
For the passive case we have adopted a Lagrangian code
which explicitly which preserves the symmetries of the conformation tensor
(see Appendix A).