



Next: Active polymers
Up: Passive polymers
Previous: Coiled state
Contents
Stretched state
As the Weissenberg number exceeds unity,
the linear relaxation of polymers is no more able to
overcome the average stretching of velocity gradients.
On the contrary polymers start to elongate exponentially, and the
statistics of the conformation tensor does not reach a steady state.
The pdf of the trace of conformation tensor
becomes unsteady, with a power-law tail which keeps
moving to higher elongations (see Fig. 4.3).
Figure 4.3:
Pdfs of polymer square elongation for
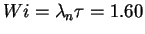 at different times:
at different times:
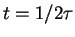 (solid line),
(solid line),
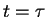 (dashed line),
(dashed line),
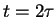 (dotted line),
(dotted line),
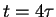 (dash-dotted line).
Above the coil-stretch transition,
the pdf of elongations becomes unsteady
(dash-dotted line).
Above the coil-stretch transition,
the pdf of elongations becomes unsteady
|
|
All the moments of conformation tensor statistics
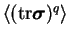 grow exponentially in time, according to
grow exponentially in time, according to
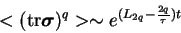 |
(4.16) |
In Figure (4.4) we show the exponential growth
of the mean square elongation
 for
for
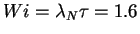 , compared
with the prediction (4.16).
Here
, compared
with the prediction (4.16).
Here 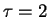 , and the value of the
generalized Lyapunov exponent
, and the value of the
generalized Lyapunov exponent
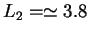 has been obtained according to
has been obtained according to
![$L_{2q}=\max_{\gamma}[2q\gamma-S(\gamma)]$](img630.png) .
For comparison we show also the steady state
in a coiled case (
.
For comparison we show also the steady state
in a coiled case (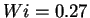 ).
).
This ``coil-stretch'' transition signals the breakdown of linear
passive theory.
Accounting for the nonlinear elastic modulus of
polymer molecules allows to recover a stationary statistics and to
develop a consistent theory of passive polymers at all Weissenberg numbers
[78]. In the following we do not pursue that approach, but we rather
focus on a different mechanism that limits polymer elongation:
the feedback of polymers on the advecting flow.
Figure:
Mean square elongation
 of passive polymers as a function of time.
In the stretched case (
of passive polymers as a function of time.
In the stretched case (
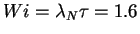 solid line) the
mean square elongation grows exponentially
according to Eq. (4.16) (dash dotted line),
while in the coiled case (
solid line) the
mean square elongation grows exponentially
according to Eq. (4.16) (dash dotted line),
while in the coiled case (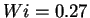 dashed line)
it reaches a statistically steady state.
dashed line)
it reaches a statistically steady state.
|
|




Next: Active polymers
Up: Passive polymers
Previous: Coiled state
Contents
Stefano Musacchio
2004-01-09
![\includegraphics[draft=false, scale=0.7]{P_pdfstretch.eps}](img625.png)
![\includegraphics[draft=false, scale=0.7]{P_pdfstretch.eps}](img625.png)
![\includegraphics[draft=false, scale=0.7]{P_stretch.eps}](img631.png)