



Next: Stretched state
Up: Passive polymers
Previous: Passive polymers
Contents
Coiled state
Below the coil-stretch transition,
at 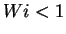 the polymer molecules spend most of the time
in a coiled state, and stretch occasionally by a considerable amount
with a strongly intermittent behavior (see Figure 4.1).
the polymer molecules spend most of the time
in a coiled state, and stretch occasionally by a considerable amount
with a strongly intermittent behavior (see Figure 4.1).
Figure:
Mean square elongation
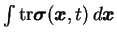 of passive polymers as a function of time.
Even in the coiled state (
of passive polymers as a function of time.
Even in the coiled state (
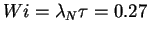 )
polymers may experience strong elongations.
)
polymers may experience strong elongations.
|
|
Following Balkovsky et al [54] Equation (4.2)
for the conformation tensor can be written in the Lagrangian reference
frame as:
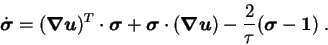 |
(4.5) |
where conformation tensor
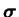 and
the velocity gradients
and
the velocity gradients
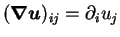 are valued along the Lagrangian trajectory
are valued along the Lagrangian trajectory
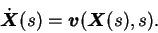 |
(4.6) |
The value of the conformation tensor can be obtained following
backward in time the Lagrangian trajectory which satisfies the
condition
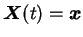 as:
as:
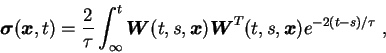 |
(4.7) |
The Lagrangian mapping matrix
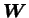 , defined by the relations
, defined by the relations
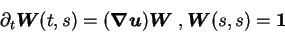 |
(4.8) |
describes the deformation of an infinitesimal fluid element along
a given Lagrangian trajectory.
The meaning of Eq. (4.7) is clear: the value of the
conformation tensor at a given time is determined by the stretching
due to velocity gradients that it has experienced during its past history,
modulated by its exponential relaxation toward the equilibrium
configuration.
The matrix
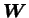 can be decomposed as
can be decomposed as
 |
(4.9) |
where
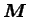 and
and
 are orthogonal matrices,
and
are orthogonal matrices,
and
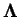 is diagonal.
Incompressibility of the flow imposes the condition
is diagonal.
Incompressibility of the flow imposes the condition
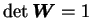 ,
and consequently the diagonal elements of
,
and consequently the diagonal elements of
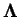 can be written as
can be written as
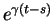 and
and
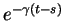 ,
where
,
where 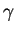 is the finite-time Lyapunov exponent at time
is the finite-time Lyapunov exponent at time 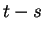 .
For time larger than the times correlation of velocity gradients
the eigenvectors of the matrix
.
For time larger than the times correlation of velocity gradients
the eigenvectors of the matrix
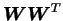 tend to the directions of the Lyapunov vectors, the matrix
tend to the directions of the Lyapunov vectors, the matrix
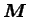 became almost time-independent, and the finite-time
Lyapunov exponents
became almost time-independent, and the finite-time
Lyapunov exponents 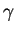 fluctuate around the value of the
leading Lyapunov exponent
fluctuate around the value of the
leading Lyapunov exponent 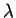 .
The trace of the conformation tensor can thus be written as
.
The trace of the conformation tensor can thus be written as
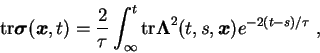 |
(4.10) |
This allows to obtain a lower bound for the square polymer elongations.
Since incompressibility imposes
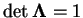 the eigenvalues of
the eigenvalues of
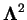 can be written as
can be written as 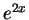 and
and 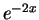 .
This leads to the inequality
.
This leads to the inequality
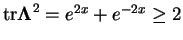 which together with
Eq. (4.10) gives the bound for the trace of the conformation tensor:
which together with
Eq. (4.10) gives the bound for the trace of the conformation tensor:
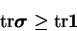 |
(4.11) |
Moreover Eq (4.10) allows to evaluate the statistics
of polymer elongations in term of the statistics of finite-time
Lyapunov exponents
![$P(\gamma,t)\propto \exp[-t S(\gamma)]$](img617.png) as:
as:
![\begin{displaymath}
< (\textrm{tr}{\mbox{\boldmath$\sigma$}})^q > \sim \int d\ga...
... S(\gamma) - 2q \left(\gamma - {1 \over \tau} \right) \right]}
\end{displaymath}](img618.png) |
(4.12) |
where 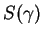 is the Cramér rate function (see, e.g., Ref. [73]).
Intense stretching events give contributions to the right tail of the
probability density function of
is the Cramér rate function (see, e.g., Ref. [73]).
Intense stretching events give contributions to the right tail of the
probability density function of
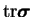 leading to the
power law prediction:
leading to the
power law prediction:
 |
(4.13) |
The exponent 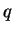 is related to the probability
of finite-time Lyapunov exponents via the equation
is related to the probability
of finite-time Lyapunov exponents via the equation
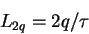 |
(4.14) |
where
![\begin{displaymath}
L_{2q}=\max_{\gamma}[2q\gamma-S(\gamma)]
\end{displaymath}](img621.png) |
(4.15) |
is the generalized Lyapunov exponent of order 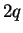 .
The convexity of the Cramér rate function
.
The convexity of the Cramér rate function 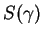 ensures
the positivity of
ensures
the positivity of 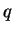 for
for 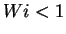 .
.
Since the distribution of polymer elongations is not accessible
experimentally, in order to validate the theory it is necessary
to resort to numerical simulations.
Eckhardt et al. in Ref. [77] have given the first evidence
of a power law tail for the
probability distribution function of
polymer elongation in three-dimensional shear turbulence.
As shown in Fig. 4.2, in our two-dimensional simulations
we observe a neat power law as well.
Figure 4.2:
Power law tail of the probability density
function of polymer square elongation,
in the passive case 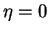 .
The Weissenberg number is
.
The Weissenberg number is 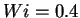 ,
quite below the coil-stretch transition.
The power law
,
quite below the coil-stretch transition.
The power law
 with the value
with the value
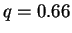 (numerically obtained from the relation
(numerically obtained from the relation
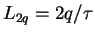 )
is drawn for comparison. In the inset, the corresponding
Cramér function
)
is drawn for comparison. In the inset, the corresponding
Cramér function 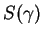 . Its minimum is
. Its minimum is
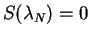 ,
with
,
with
 .
.
|
|
In order to check whether the observed exponent coincides with
the prediction (4.14) we have also
performed direct numerical simulations of particle
trajectories, and measured the probability distribution of finite-time
Lyapunov exponents, thereby obtaining the expected 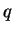 .
The numerical result is in close agreement with theory.
.
The numerical result is in close agreement with theory.




Next: Stretched state
Up: Passive polymers
Previous: Passive polymers
Contents
Stefano Musacchio
2004-01-09
![]() the polymer molecules spend most of the time
in a coiled state, and stretch occasionally by a considerable amount
with a strongly intermittent behavior (see Figure 4.1).
the polymer molecules spend most of the time
in a coiled state, and stretch occasionally by a considerable amount
with a strongly intermittent behavior (see Figure 4.1).
![\includegraphics[draft=false, scale=0.7]{P_coiled.eps}](img595.png)
![]() can be decomposed as
can be decomposed as
![]() the eigenvalues of
the eigenvalues of
![]() can be written as
can be written as ![]() and
and ![]() .
This leads to the inequality
.
This leads to the inequality
![]() which together with
Eq. (4.10) gives the bound for the trace of the conformation tensor:
which together with
Eq. (4.10) gives the bound for the trace of the conformation tensor:
![]() as:
as:
![\includegraphics[draft=false, scale=0.7]{P_pdftraccia.eps}](img624.png)
![]() .
The numerical result is in close agreement with theory.
.
The numerical result is in close agreement with theory.