



Next: Summary
Up: Active polymers
Previous: Decaying turbulence
Contents
Inverse energy cascade
The strong influence of polymers on the energy balance
pose the intriguing question of the possible effects on the inverse
energy cascade which occurs in the Newtonian case.
Indeed, in absence of friction, the growth rate of kinetic energy
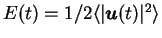 can be obtained repeating the derivation of the energy balance (4.17)
but averaging only over space and over the statistics of the
random forcing
can be obtained repeating the derivation of the energy balance (4.17)
but averaging only over space and over the statistics of the
random forcing
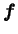 :
:
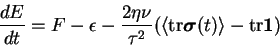 |
(4.20) |
As already shown, the polymer contribution has a definite sign,
acting as a dissipative term. Neglecting the
viscous dissipation 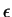 , which in the limit of
infinite Reynolds number is vanishingly small, it is clear from
Eq. (4.20) that the energy growth rate in the viscoelastic case
is reduced with respect to the Newtonian case where it is
essentially given by the input of the random forcing.
, which in the limit of
infinite Reynolds number is vanishingly small, it is clear from
Eq. (4.20) that the energy growth rate in the viscoelastic case
is reduced with respect to the Newtonian case where it is
essentially given by the input of the random forcing.
In order to measure the energy growth rate, I performed
numerical simulations of the viscoelastic model
using a slightly different configuration: I
turned off the friction term and put the forcing on a smaller scale,
allowing the energy to give origin to an inverse cascade.
After an initial growth, the polymer
elongation reaches indeed a statistically steady state, and consequently
the energy growth rate is reduced of a constant fraction depending on the
concentration and the Weissenberg number of the polymer solution,
in quantitative agreement with Eq. (4.20) (see Fig. (4.11)).
Figure 4.11:
Linear growth of kinetic energy growth in absence of friction.
The energy growth rate is reduced by the polymer feedback at
increasing 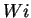 number. If the Weissenberg number is large
enough the energy growth can be completely stopped.
number. If the Weissenberg number is large
enough the energy growth can be completely stopped.
|
|
We remark the striking fact that at
sufficiently high 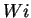 numbers, the energy growth rate
in the viscoelastic case can be reduced to zero when the
polymer dissipation balances exactly the forcing input.
This means that the inverse cascade can be
completely suppressed by the polymer feedback even in
absence of friction.
numbers, the energy growth rate
in the viscoelastic case can be reduced to zero when the
polymer dissipation balances exactly the forcing input.
This means that the inverse cascade can be
completely suppressed by the polymer feedback even in
absence of friction.
The feedback of polymers reacts on the fluid in order to reduce
its velocity gradients. In the case of two-dimensional turbulence
the power spectrum of velocity gradients is peaked at the forcing
length-scale, thus is reasonable to assume that polymer feedback
is essentially localized at the scale of forcing and does
not entail the inertial range.
Thus we expect to observe also for the viscoelastic
two-dimensional solution the development of the inverse cascade,
with a constant flux
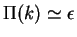 reduced of a fraction depending on the elongation of the polymers:
reduced of a fraction depending on the elongation of the polymers:
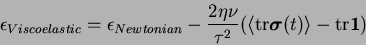 |
(4.21) |
Figure 4.12:
Inverse energy cascade in viscoelastic simulations.
Increasing the 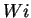 number the energy flux in the cascade
is reduced and consequently the friction term stops the cascade
at smaller scale.
number the energy flux in the cascade
is reduced and consequently the friction term stops the cascade
at smaller scale.
|
|
A direct measurement of the energy flux requires a large scaling range in the
inverse energy cascade, but at the same time it is necessary
to resolve also the direct enstrophy cascade whose smooth flow is responsible
of the polymer stretching. Unfortunately this task is unaffordable
with actual computational resource. Nevertheless it is possible to have an
indirect check of our prediction. The hypothesis of an inverse cascade
with constant energy flux, leads to a Kolmogorov-like scaling law
for the velocity fluctuations
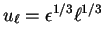 with the reduced flux given by Eq. (4.21).
The friction length scale
with the reduced flux given by Eq. (4.21).
The friction length scale 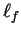 where the
friction term balance the nonlinear term responsible for
the energy transfer, can be estimated by dimensional arguments
(see Chapter 1) as
where the
friction term balance the nonlinear term responsible for
the energy transfer, can be estimated by dimensional arguments
(see Chapter 1) as
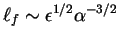 .
The reduction of the energy flux in the viscoelastic case should then
reflect in a reduction of the friction length-scale.
Restoring the friction term in our simulations, we checked
that at increasing values of
.
The reduction of the energy flux in the viscoelastic case should then
reflect in a reduction of the friction length-scale.
Restoring the friction term in our simulations, we checked
that at increasing values of 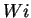 number the inverse energy cascade is indeed
stopped by friction at smaller scale as shown in Figure (4.12).
number the inverse energy cascade is indeed
stopped by friction at smaller scale as shown in Figure (4.12).
While the mean square polymer elongation
 quickly reaches statistically
constant values depending on the value of
quickly reaches statistically
constant values depending on the value of 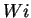 , the
kinetic energy grows up with different rates until
it reaches the steady state fixed by the energy balance (4.17)
(see Figure (4.13))
, the
kinetic energy grows up with different rates until
it reaches the steady state fixed by the energy balance (4.17)
(see Figure (4.13))
Figure 4.13:
Average kinetic energy in viscoelastic
simulations of the inverse energy cascade.
In the initial stage the energy grows linearly with smaller
rates at larger 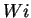 numbers then it is stopped by
the friction term at values determined by the energy
balance (4.17)
numbers then it is stopped by
the friction term at values determined by the energy
balance (4.17)
|
|




Next: Summary
Up: Active polymers
Previous: Decaying turbulence
Contents
Stefano Musacchio
2004-01-09
![]() can be obtained repeating the derivation of the energy balance (4.17)
but averaging only over space and over the statistics of the
random forcing
can be obtained repeating the derivation of the energy balance (4.17)
but averaging only over space and over the statistics of the
random forcing
![]() :
:
![\includegraphics[draft=false,scale=0.7]{P_inversa0.eps}](img685.png)
![]() numbers, the energy growth rate
in the viscoelastic case can be reduced to zero when the
polymer dissipation balances exactly the forcing input.
This means that the inverse cascade can be
completely suppressed by the polymer feedback even in
absence of friction.
numbers, the energy growth rate
in the viscoelastic case can be reduced to zero when the
polymer dissipation balances exactly the forcing input.
This means that the inverse cascade can be
completely suppressed by the polymer feedback even in
absence of friction.
![]() reduced of a fraction depending on the elongation of the polymers:
reduced of a fraction depending on the elongation of the polymers:
![\includegraphics[draft=false,scale=0.7]{P_inversa3.eps}](img688.png)
![]() quickly reaches statistically
constant values depending on the value of
quickly reaches statistically
constant values depending on the value of ![]() , the
kinetic energy grows up with different rates until
it reaches the steady state fixed by the energy balance (4.17)
(see Figure (4.13))
, the
kinetic energy grows up with different rates until
it reaches the steady state fixed by the energy balance (4.17)
(see Figure (4.13))
![\includegraphics[draft=false,scale=0.7]{P_inversa1.eps}](img693.png)